当存在一条以中点为端点的线段时穿越火线辅助技巧,常常将这条线段对折以构造全等三角形。
当我们遇到线段中点的问题时穿越火线辅助技巧,我们常常会考虑将线段的长度加倍。 构造的三角形将与之前的三角形全等。 接下来就很容易证明这一点了。 让我们看看下面这个主题,以便更好地理解它。
例:已知,如图所示,AD为△ABC的中心线,且∠1=∠2,∠3=∠4。 验证:BE+CF>EF
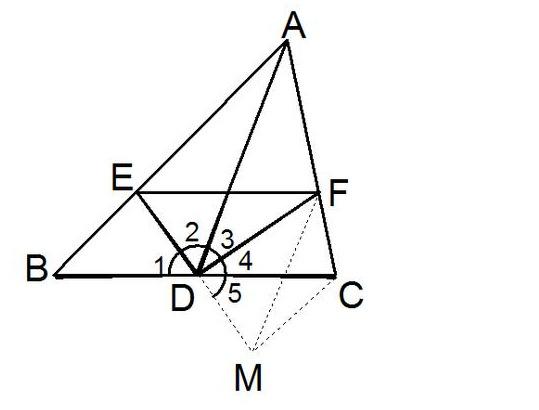
如果这道题有中间线,可以用这种辅助线法。 解决方法如下:
证明:将ED扩展到M,令DM=DE,连接CM、FM△BDE和△CDM,BD=CD∠1=∠5ED=MD∴△BDE≌△CDM∴CM=BE且∵∠1=∠2, ∠3 = ∠4∠1+∠2+∠3 + ∠4 = 180度 ∴∠3 + ∠2 = 90度,即∠EDF = 90度 ∴∠FDM = ∠EDF = 90度 △EDF和△MDF ED = MD∠FDM = ∠EDFDF = DF∴△EDF≌△MDF∴EF = MF∵ 在△CMF中,CF+CM>MFBE+CF>EF
当三角形中有中线时,通常将中线加倍以构造全等三角形。
例:已知,如图所示,AD为△ABC的中线。 验证:AB+AC>2AD
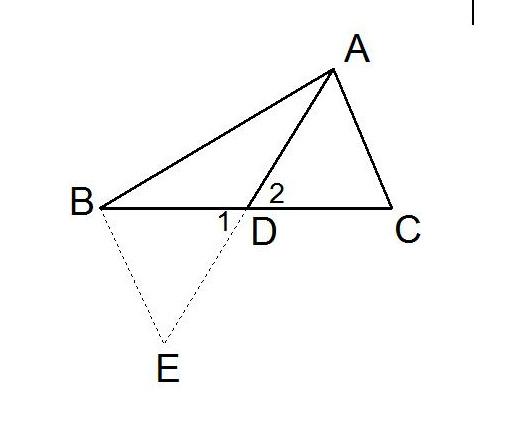
证明:将AD延伸至E,令DE = AD,将BE∵AD与△ACD和△EBD中的△ABC ∴BD = CD的中线相连 BD = CD∠1 = ∠2AD = ED∴△ACD≌△EBD∵△ ABE中有AB+BE>AE∴AB+AC>2AD
角平分线通常在角的两侧截取相等的线段以构造全等三角形。
已知,如图所示,AD为△ABC的中心线且∠1=∠2,∠3=∠4。 验证:BE+CF>EF
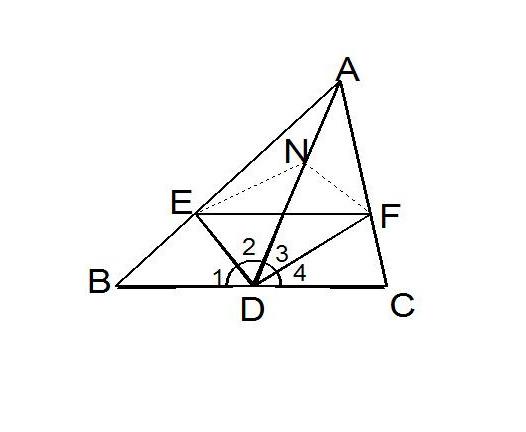
证明:在DA上截取DN=DB并连接NE和NF,则在△BDE和△NDE中DN=DC,DN=DB∠1=∠2ED=ED∴△BDE≌△NDE∴BE=NE。 同理可证:CF=NF于△EFN,EN+FN>EF∴BE+CF>EF
今天介绍一下三角形中线和角平分线常用的辅助线。 做了辅助线之后,问题就变得很简单了。 如果我们根据已知条件来分析寻找辅助线的方法,时间会变得更短。 这需要很长的时间,但是如果我们总结一下规则,就会节省很多时间。 我们可以适当改变已经证明的题,做到解决一题掌握一类题,提高举一反三、灵活应变的能力。
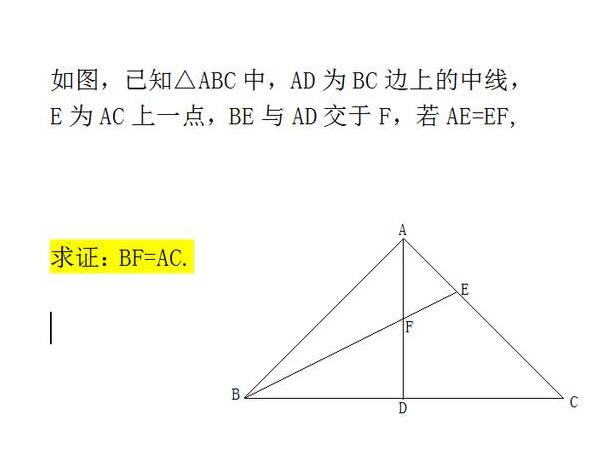
最后,我给大家提一个问题,让大家思考一下。 将以上内容与评论中你的方法结合起来。 问题如下图所示。
我们做数学证明题或者计算题的时候,经常需要做辅助线。 有些题的辅助线制作起来很容易,根据已知的条件就可以轻松制作。 然而,对于一些问题,我们却需要很长时间才能找到。 辅助线的练习,但数学是一门学科。 经过这么多年的发展,出现了一些经典的问题。 我们经常针对一些题总结并找到常用的辅助线做法。 今天我们来说说一些与三角形中心线和角平分线相关的辅助线。
当存在一条以中点为端点的线段时,常常将这条线段对折以构造全等三角形。
当我们遇到线段中点的问题时,我们常常会考虑将线段的长度加倍。 构造的三角形将与之前的三角形全等。 接下来就很容易证明了。 让我们看看下面这个主题,以便更好地理解它。
例:已知穿越火线辅助技巧,如图所示,AD为△ABC的中心线,且∠1=∠2,∠3=∠4。 验证:BE+CF>EF
如果这道题有中间线,可以用这种辅助线法。 解决方法如下:
证明:将ED扩展到M,令DM=DE,连接CM、FM△BDE和△CDM,BD=CD∠1=∠5ED=MD∴△BDE≌△CDM∴CM=BE且∵∠1=∠2, ∠3 = ∠4∠1+∠2+∠3 + ∠4 = 180度 ∴∠3 + ∠2 = 90度,即∠EDF = 90度 ∴∠FDM = ∠EDF = 90度 △EDF和△MDF ED = MD∠FDM = ∠EDFDF = DF∴△EDF≌△MDF∴EF = MF∵ 在△CMF中,CF+CM>MFBE+CF>EF
当三角形中有中线时,通常将中线加倍以构造全等三角形。
例:已知,如图所示,AD为△ABC的中线。 验证:AB+AC>2AD
证明:将AD延伸至E,令DE = AD,将BE∵AD连为△ACD和△EBD中△ABC ∴BD = CD的中线 BD = CD∠1 = ∠2AD = ED∴△ACD≌△EBD∵△ ABE中有AB+BE>AE∴AB+AC>2AD
角平分线通常在角的两侧截取相等的线段以构造全等三角形。
已知,如图所示,AD为△ABC的中心线且∠1=∠2,∠3=∠4。 验证:BE+CF>EF
证明:在DA上截取DN=DB并连接NE和NF,则在△BDE和△NDE中DN=DC,DN=DB∠1=∠2ED=ED∴△BDE≌△NDE∴BE=NE。 同理可证:CF=NF于△EFN,EN+FN>EF∴BE+CF>EF
今天介绍一下三角形中线和角平分线常用的辅助线。 做了辅助线之后,问题就变得很简单了。 如果我们根据已知条件来分析寻找辅助线的方法,时间会变得更短。 这需要很长的时间,但是如果我们总结一下规则穿越火线辅助技巧,就会节省很多时间。 我们可以适当改变已经证明的题,做到解决一题掌握一类题,提高举一反三、灵活应变的能力。
最后,我给大家提一个问题,让大家思考一下。 将以上内容与评论中你的方法结合起来。 问题如下图所示。